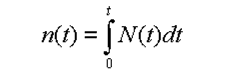
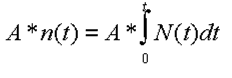
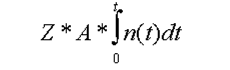
Prof. Dr. Dieter Röß - Workshop für Firmengründer WS 95/96
Die Bank zahlt z % Zinsen
z = opportunity cost 4 plus
Inflationsrate plus Risikozuschlag .
Der Zinssatz z wird am Geldmarkt aus Angebot und Nachfrage bestimmt. Der Ausleiher (z.B. eine Bank) garantiert den ausgemachten Zinssatz und die Rückzahlung des eingesetzten Kapitals zum ausgemachten Zeitpunkt.
Der wundersame Geld-Vermehrer zahlt einen viel höheren Zinssatz : Z >> z
Alle Leute drängen ihm ihr Geld auf
(Ostdeutschland nach der Wende, zur Zeit Bulgarien, Anfang '93 Roma im Saarland 5 ).
Wir rechnen zur besseren Übersichtlichkeit mit kontinuierlichen Größen (Zinszahlungen sind normalerweise periodisch, was die Rechnung weniger übersichtlich werden läßt).
| Typische Einzahlung | A |
| Anleger pro Zeiteinheit | N(t) |
| Anleger nach Zeit t | 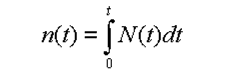 |
| Eingesammeltes Geld nach der Zeit t | 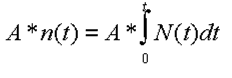 |
| Aufgelaufene Zinsschulden | 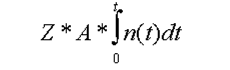 |
Damit die laufenden Zinsen aus dem laufend eingesammelten Kapital bedient werden können, muß sein:
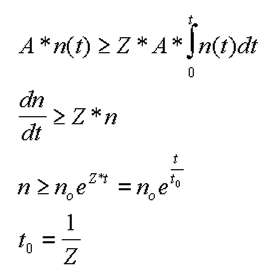
Das System erfordert also eine exponentiell anwachsende Einlegerschar. Das Verhängnisvolle ist, daß selbst bei sehr hoher Verzinsung (Z=50%) ein relativ mäßiges Wachstum um den Faktor e½ = 1,65 in einem Jahr genügt, um die aus Zinsforderungen resultierenden Zahlungen aus dem Kapital zu leisten (nicht berücksichtigt sind dabei die "Kosten" des Geldeintreibers).
Daß für die Zinszahlungen das Kapital verwendet wird, merken die Anleger nicht.
Da das Wachstum solcher schwindelhafter Anlegerlawinen immer sehr viel höher ist als 65 % pro Jahr, können am Anfang auch einzelne, ängstliche Anleger ausbezahlt werden, während sich gleichzeitig ein großes Kapital anhäuft.
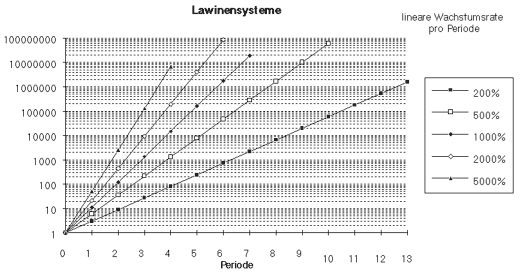
Die Graphik zeigt die Zahl der Teilnehmer in einer exponentiell wachsenden Lawine für praktisch vorstellbare Wachstumsraten. Man sieht, daß bereits innerhalb weniger Perioden riesige Zahlen zustandekommen, welche das Abbrechen der Lawine erzwingen (in praxi wird die Lawine am Anfang extrem schnell wachsen, so daß die angenommene Ausgangszahl 1 gleichmäßigen, exponentiellen Wachstums vielleicht mit einem Faktor 100 - 1000 zu multiplizieren wäre).
Wenn der Bruchteil a (Alpha) der Anleger in der Zeiteinheit sein Geld zurückfordert, gilt:
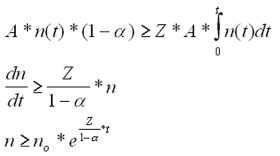
Wird vom Geldvermehrer das Kapital mit dem Marktzins z angelegt, dann ist der effektive, exponentielle Faktor (Z-z), was bei den hohen, versprochenen Zinsen gar keinen großen Unterschied ausmacht!
Eine genauere, wie üblich diskontinuierliche Periodenrechnung
zeigt:
In der ersten Periode sind überhaupt keine Zinszahlungen fällig;
hier kann man jeden Zins versprechen.
Die Zahlenbeispiele zeigen aber auch, daß man in der Praxis selbst bei sehr hohen Zinsen so lange die Zinsen aus dem Kapital bedienen kann, wie das Wachstum der Lawine anhält. Dies macht es für die Behörden sehr schwer, den entsprechenden Betrügern das Handwerk frühzeitig zu legen und
Tatsächlich muß man sich ja fragen, ob die Betrogenen nicht auch selbst Betrüger sind, da ja niemand wirklich glauben kann, daß ein anderer ihm 50% Zinsen zahlt, wenn er auf der Bank das gleiche Geld für höchstens 12 % bekommen kann! Die Anleger sehen sich aber nicht als Betrüger, weil für sie nicht klar ersichtlich ist, wen sie eigentlich betrügen: sie vermuten wohl, es seien die Späteren in der Lawine, darum muß man sofort zugreifen!, tatsächlich sind sie mit aller Wahrscheinlichkeit ja selbst die Betrogenen 6.
Für den Initiator ist es ein Optimierungsspiel, wann er am besten mit dem eingesammelten Geld in Südamerika verschwindet. Der für ihn richtige Zeitpunkt ist erreicht,
4 1995: opportunity
cost: sind die Gewinne, die man mit einer Alternative hätte erzielen
können. Dies entspricht der Prämie für den Verzicht auf
die eigene Nutzung von verliehenem Geld. [zurück]
5 20.6.1997: 1996/1997 Albanien; dies führte nahezu zum
Zusammenbruch des Staates; noch 1998 meint die Regierung, sie müsse
die so entstandenen Verluste ausgleichen, um schlimmeres zu verhindern;
1997-1998 Rußland. [zurück]
6 1995: Ähnlich zwiespältig sehe ich die Haltung vieler
Bürger gegenüber Staat und Sozialsystemen. [zurück]